10. Statistical inference#
10.1. Overview#
A typical data analysis task in practice is to draw conclusions about some unknown aspect of a population of interest based on observed data sampled from that population; we typically do not get data on the entire population. Data analysis questions regarding how summaries, patterns, trends, or relationships in a data set extend to the wider population are called inferential questions. This chapter will start with the fundamental ideas of sampling from populations and then introduce two common techniques in statistical inference: point estimation and interval estimation.
10.2. Chapter learning objectives#
By the end of the chapter, readers will be able to do the following:
Describe real-world examples of questions that can be answered with statistical inference.
Define common population parameters (e.g., mean, proportion, standard deviation) that are often estimated using sampled data, and estimate these from a sample.
Define the following statistical sampling terms: population, sample, population parameter, point estimate, and sampling distribution.
Explain the difference between a population parameter and a sample point estimate.
Use Python to draw random samples from a finite population.
Use Python to create a sampling distribution from a finite population.
Describe how sample size influences the sampling distribution.
Define bootstrapping.
Use Python to create a bootstrap distribution to approximate a sampling distribution.
Contrast the bootstrap and sampling distributions.
10.3. Why do we need sampling?#
We often need to understand how quantities we observe in a subset of data relate to the same quantities in the broader population. For example, suppose a retailer is considering selling iPhone accessories, and they want to estimate how big the market might be. Additionally, they want to strategize how they can market their products on North American college and university campuses. This retailer might formulate the following question:
What proportion of all undergraduate students in North America own an iPhone?
In the above question, we are interested in making a conclusion about all undergraduate students in North America; this is referred to as the population. In general, the population is the complete collection of individuals or cases we are interested in studying. Further, in the above question, we are interested in computing a quantity—the proportion of iPhone owners—based on the entire population. This proportion is referred to as a population parameter. In general, a population parameter is a numerical characteristic of the entire population. To compute this number in the example above, we would need to ask every single undergraduate in North America whether they own an iPhone. In practice, directly computing population parameters is often time-consuming and costly, and sometimes impossible.
A more practical approach would be to make measurements for a sample, i.e., a subset of individuals collected from the population. We can then compute a sample estimate—a numerical characteristic of the sample—that estimates the population parameter. For example, suppose we randomly selected ten undergraduate students across North America (the sample) and computed the proportion of those students who own an iPhone (the sample estimate). In that case, we might suspect that proportion is a reasonable estimate of the proportion of students who own an iPhone in the entire population. Fig. 10.1 illustrates this process. In general, the process of using a sample to make a conclusion about the broader population from which it is taken is referred to as statistical inference.
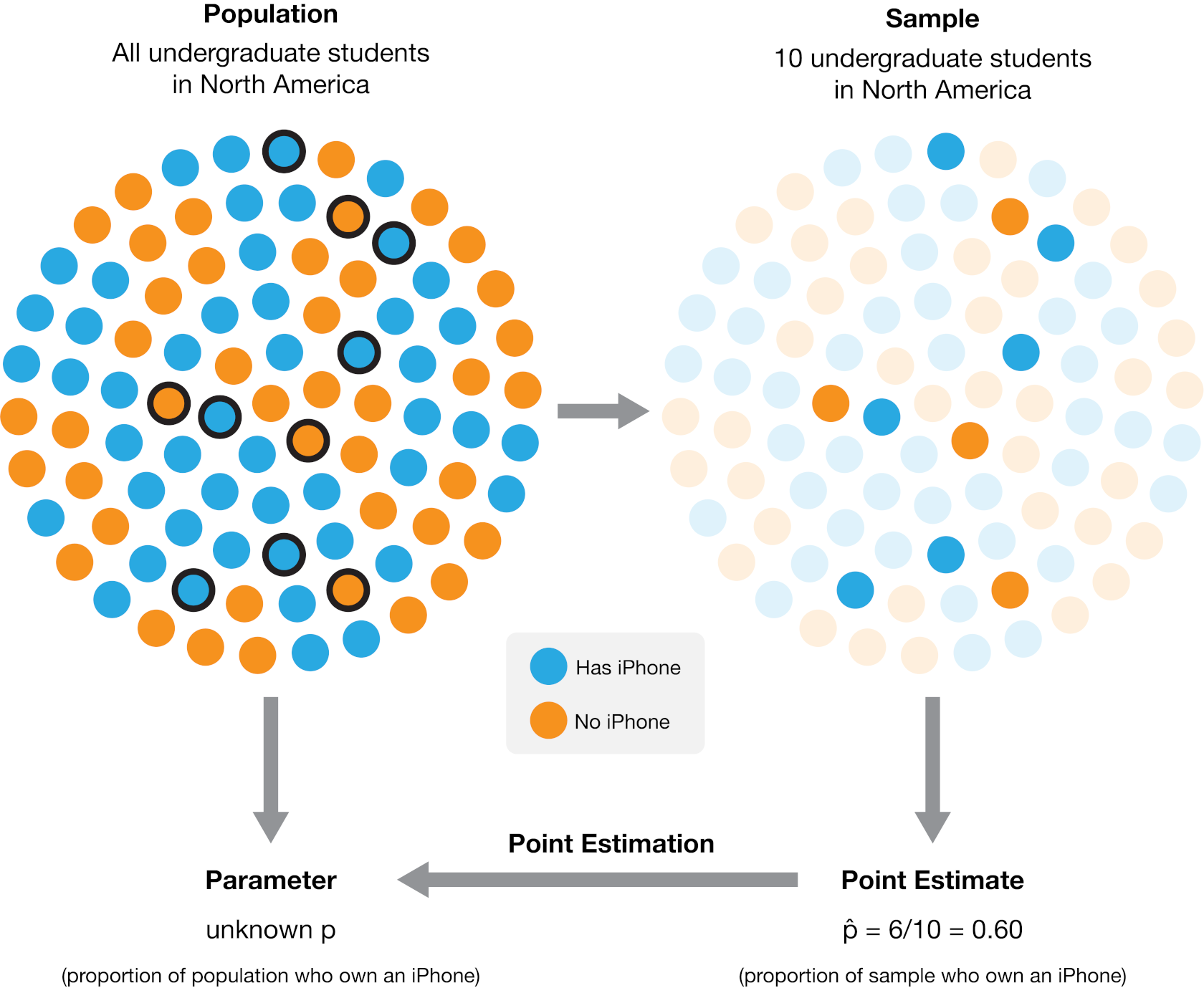
Fig. 10.1 The process of using a sample from a broader population to obtain a point estimate of a population parameter. In this case, a sample of 10 individuals yielded 6 who own an iPhone, resulting in an estimated population proportion of 60% iPhone owners. The actual population proportion in this example illustration is 53.8%.#
Note that proportions are not the only kind of population parameter we might be interested in. For example, suppose an undergraduate student studying at the University of British Columbia in Canada is looking for an apartment to rent. They need to create a budget, so they want to know something about studio apartment rental prices in Vancouver, BC. This student might formulate the following question:
What is the average price-per-month of studio apartment rentals in Vancouver, Canada?
In this case, the population consists of all studio apartment rentals in Vancouver, and the population parameter is the average price-per-month. Here we used the average as a measure of the center to describe the “typical value” of studio apartment rental prices. But even within this one example, we could also be interested in many other population parameters. For instance, we know that not every studio apartment rental in Vancouver will have the same price per month. The student might be interested in how much monthly prices vary and want to find a measure of the rentals’ spread (or variability), such as the standard deviation. Or perhaps the student might be interested in the fraction of studio apartment rentals that cost more than $1000 per month. The question we want to answer will help us determine the parameter we want to estimate. If we were somehow able to observe the whole population of studio apartment rental offerings in Vancouver, we could compute each of these numbers exactly; therefore, these are all population parameters. There are many kinds of observations and population parameters that you will run into in practice, but in this chapter, we will focus on two settings:
Using categorical observations to estimate the proportion of a category
Using quantitative observations to estimate the average (or mean)
10.4. Sampling distributions#
10.4.1. Sampling distributions for proportions#
We will look at an example using data from Inside Airbnb [Cox, n.d.]. Airbnb is an online marketplace for arranging vacation rentals and places to stay. The data set contains listings for Vancouver, Canada, in September 2020. Our data includes an ID number, neighborhood, type of room, the number of people the rental accommodates, number of bathrooms, bedrooms, beds, and the price per night.
import pandas as pd
airbnb = pd.read_csv("data/listings.csv")
airbnb
| id | neighbourhood | room_type | accommodates | bathrooms | bedrooms | beds | price | |
|---|---|---|---|---|---|---|---|---|
| 0 | 1 | Downtown | Entire home/apt | 5 | 2 baths | 2 | 2 | 150.00 |
| 1 | 2 | Downtown Eastside | Entire home/apt | 4 | 2 baths | 2 | 2 | 132.00 |
| 2 | 3 | West End | Entire home/apt | 2 | 1 bath | 1 | 1 | 85.00 |
| 3 | 4 | Kensington-Cedar Cottage | Entire home/apt | 2 | 1 bath | 1 | 0 | 146.00 |
| 4 | 5 | Kensington-Cedar Cottage | Entire home/apt | 4 | 1 bath | 1 | 2 | 110.00 |
| ... | ... | ... | ... | ... | ... | ... | ... | ... |
| 4589 | 4590 | Downtown Eastside | Entire home/apt | 5 | 1 bath | 1 | 1 | 99.00 |
| 4590 | 4591 | Oakridge | Private room | 2 | 1.5 baths | 1 | 1 | 42.51 |
| 4591 | 4592 | Dunbar Southlands | Private room | 2 | 1.5 shared baths | 1 | 1 | 53.29 |
| 4592 | 4593 | West End | Entire home/apt | 4 | 1 bath | 2 | 2 | 145.00 |
| 4593 | 4594 | Shaughnessy | Entire home/apt | 6 | 1 bath | 3 | 4 | 135.00 |
4594 rows × 8 columns
Suppose the city of Vancouver wants information about Airbnb rentals to help
plan city bylaws, and they want to know how many Airbnb places are listed as
entire homes and apartments (rather than as private or shared rooms). Therefore
they may want to estimate the true proportion of all Airbnb listings where the
room type is listed as “entire home or apartment.” Of course, we usually
do not have access to the true population, but here let’s imagine (for learning
purposes) that our data set represents the population of all Airbnb rental
listings in Vancouver, Canada.
We can find the proportion of listings for each room type
by using the value_counts function with the normalize parameter
as we did in previous chapters.
airbnb["room_type"].value_counts(normalize=True)
room_type
Entire home/apt 0.747497
Private room 0.246408
Shared room 0.005224
Hotel room 0.000871
Name: proportion, dtype: float64
We can see that the proportion of Entire home/apt listings in
the data set is 0.747. This
value, 0.747, is the population parameter. Remember, this
parameter value is usually unknown in real data analysis problems, as it is
typically not possible to make measurements for an entire population.
Instead, perhaps we can approximate it with a small subset of data!
To investigate this idea, let’s try randomly selecting 40 listings (i.e., taking a random sample of
size 40 from our population), and computing the proportion for that sample.
We will use the sample method of the DataFrame
object to take the sample. The argument n of sample is the size of the sample to take
and since we are starting to use randomness here,
we are also setting the random seed via numpy to make the results reproducible.
import numpy as np
np.random.seed(155)
airbnb.sample(n=40)["room_type"].value_counts(normalize=True)
room_type
Entire home/apt 0.725
Private room 0.250
Shared room 0.025
Name: proportion, dtype: float64
Here we see that the proportion of entire home/apartment listings in this random sample is 0.725. Wow—that’s close to our true population value! But remember, we computed the proportion using a random sample of size 40. This has two consequences. First, this value is only an estimate, i.e., our best guess of our population parameter using this sample. Given that we are estimating a single value here, we often refer to it as a point estimate. Second, since the sample was random, if we were to take another random sample of size 40 and compute the proportion for that sample, we would not get the same answer:
airbnb.sample(n=40)["room_type"].value_counts(normalize=True)
room_type
Entire home/apt 0.625
Private room 0.350
Shared room 0.025
Name: proportion, dtype: float64
Confirmed! We get a different value for our estimate this time. That means that our point estimate might be unreliable. Indeed, estimates vary from sample to sample due to sampling variability. But just how much should we expect the estimates of our random samples to vary? Or in other words, how much can we really trust our point estimate based on a single sample?
To understand this, we will simulate many samples (much more than just two) of size 40 from our population of listings and calculate the proportion of entire home/apartment listings in each sample. This simulation will create many sample proportions, which we can visualize using a histogram. The distribution of the estimate for all possible samples of a given size (which we commonly refer to as \(n\)) from a population is called a sampling distribution. The sampling distribution will help us see how much we would expect our sample proportions from this population to vary for samples of size 40.
We again use the sample to take samples of size 40 from our
population of Airbnb listings. But this time we use a list comprehension
to repeat the operation multiple times (as we did previously in Chapter 9).
In this case we repeat the operation 20,000 times to obtain 20,000 samples of size 40.
To make it clear which rows in the data frame come
which of the 20,000 samples, we also add a column called replicate with this information using the assign function,
introduced previously in Chapter 3.
The call to concat concatenates all the 20,000 data frames
returned from the list comprehension into a single big data frame.
samples = pd.concat([
airbnb.sample(40).assign(replicate=n)
for n in range(20_000)
])
samples
| id | neighbourhood | room_type | accommodates | bathrooms | bedrooms | beds | price | replicate | |
|---|---|---|---|---|---|---|---|---|---|
| 605 | 606 | Marpole | Entire home/apt | 3 | 1 bath | 1 | 1 | 91.0 | 0 |
| 4579 | 4580 | Downtown | Entire home/apt | 3 | 1 bath | 1 | 2 | 160.0 | 0 |
| 1739 | 1740 | West End | Entire home/apt | 2 | 1 bath | 1 | 2 | 151.0 | 0 |
| 3904 | 3905 | Oakridge | Private room | 6 | 1 private bath | 3 | 3 | 185.0 | 0 |
| 1596 | 1597 | Kitsilano | Entire home/apt | 1 | 1 bath | 1 | 1 | 99.0 | 0 |
| ... | ... | ... | ... | ... | ... | ... | ... | ... | ... |
| 3060 | 3061 | Hastings-Sunrise | Private room | 2 | 3.5 shared baths | 1 | 1 | 78.0 | 19999 |
| 527 | 528 | Kitsilano | Private room | 4 | 1 private bath | 1 | 1 | 99.0 | 19999 |
| 1587 | 1588 | Downtown | Entire home/apt | 6 | 1 bath | 1 | 3 | 169.0 | 19999 |
| 3860 | 3861 | Downtown | Entire home/apt | 3 | 1 bath | 1 | 1 | 100.0 | 19999 |
| 2747 | 2748 | Downtown | Entire home/apt | 3 | 1 bath | 1 | 1 | 285.0 | 19999 |
800000 rows × 9 columns
Since the column replicate indicates the replicate/sample number,
we can verify that we indeed seem to have 20,0000 samples
starting at sample 0 and ending at sample 19,999.
Now that we have obtained the samples, we need to compute the
proportion of entire home/apartment listings in each sample.
We first group the data by the replicate variable—to group the
set of listings in each sample together—and then use value_counts
with normalize=True to compute the proportion in each sample.
Both the first and last few entries of the resulting data frame are printed
below to show that we end up with 20,000 point estimates, one for each of the 20,000 samples.
(
samples
.groupby("replicate")
["room_type"]
.value_counts(normalize=True)
)
replicate room_type
0 Entire home/apt 0.750
Private room 0.250
1 Entire home/apt 0.775
Private room 0.225
2 Entire home/apt 0.750
...
19998 Entire home/apt 0.700
Private room 0.275
Shared room 0.025
19999 Entire home/apt 0.750
Private room 0.250
Name: proportion, Length: 44552, dtype: float64
The returned object is a series,
and as we have previously learned
we can use reset_index to change it to a data frame.
However,
there is one caveat here:
when we use the value_counts function
on a grouped series and try to reset_index
we will end up with two columns with the same name
and therefore get an error
(in this case, room_type will occur twice).
Fortunately,
there is a simple solution:
when we call reset_index,
we can specify the name of the new column
with the name parameter:
(
samples
.groupby("replicate")
["room_type"]
.value_counts(normalize=True)
.reset_index(name="sample_proportion")
)
| replicate | room_type | sample_proportion | |
|---|---|---|---|
| 0 | 0 | Entire home/apt | 0.750 |
| 1 | 0 | Private room | 0.250 |
| 2 | 1 | Entire home/apt | 0.775 |
| 3 | 1 | Private room | 0.225 |
| 4 | 2 | Entire home/apt | 0.750 |
| ... | ... | ... | ... |
| 44547 | 19998 | Entire home/apt | 0.700 |
| 44548 | 19998 | Private room | 0.275 |
| 44549 | 19998 | Shared room | 0.025 |
| 44550 | 19999 | Entire home/apt | 0.750 |
| 44551 | 19999 | Private room | 0.250 |
44552 rows × 3 columns
Below we put everything together and also filter the data frame to keep only the room types that we are interested in.
sample_estimates = (
samples
.groupby("replicate")
["room_type"]
.value_counts(normalize=True)
.reset_index(name="sample_proportion")
)
sample_estimates = sample_estimates[sample_estimates["room_type"] == "Entire home/apt"]
sample_estimates
| replicate | room_type | sample_proportion | |
|---|---|---|---|
| 0 | 0 | Entire home/apt | 0.750 |
| 2 | 1 | Entire home/apt | 0.775 |
| 4 | 2 | Entire home/apt | 0.750 |
| 6 | 3 | Entire home/apt | 0.675 |
| 8 | 4 | Entire home/apt | 0.725 |
| ... | ... | ... | ... |
| 44541 | 19995 | Entire home/apt | 0.775 |
| 44543 | 19996 | Entire home/apt | 0.750 |
| 44545 | 19997 | Entire home/apt | 0.725 |
| 44547 | 19998 | Entire home/apt | 0.700 |
| 44550 | 19999 | Entire home/apt | 0.750 |
20000 rows × 3 columns
We can now visualize the sampling distribution of sample proportions for samples of size 40 using a histogram in Fig. 10.2. Keep in mind: in the real world, we don’t have access to the full population. So we can’t take many samples and can’t actually construct or visualize the sampling distribution. We have created this particular example such that we do have access to the full population, which lets us visualize the sampling distribution directly for learning purposes.
sampling_distribution = alt.Chart(sample_estimates).mark_bar().encode(
x=alt.X("sample_proportion")
.bin(maxbins=20)
.title("Sample proportions"),
y=alt.Y("count()").title("Count"),
)
sampling_distribution
Fig. 10.2 Sampling distribution of the sample proportion for sample size 40.#
The sampling distribution in Fig. 10.2 appears to be bell-shaped, is roughly symmetric, and has one peak. It is centered around 0.75 and the sample proportions range from about 0.55 to about 0.95. In fact, we can calculate the mean of the sample proportions.
sample_estimates["sample_proportion"].mean()
0.74848375
We notice that the sample proportions are centered around the population proportion value, 0.748! In general, the mean of the sampling distribution should be equal to the population proportion. This is great news because it means that the sample proportion is neither an overestimate nor an underestimate of the population proportion. In other words, if you were to take many samples as we did above, there is no tendency towards over or underestimating the population proportion. In a real data analysis setting where you just have access to your single sample, this implies that you would suspect that your sample point estimate is roughly equally likely to be above or below the true population proportion.
10.4.2. Sampling distributions for means#
In the previous section, our variable of interest—room_type—was
categorical, and the population parameter was a proportion. As mentioned in
the chapter introduction, there are many choices of the population parameter
for each type of variable. What if we wanted to infer something about a
population of quantitative variables instead? For instance, a traveler
visiting Vancouver, Canada may wish to estimate the
population mean (or average) price per night of Airbnb listings. Knowing
the average could help them tell whether a particular listing is overpriced.
We can visualize the population distribution of the price per night with a histogram.
population_distribution = alt.Chart(airbnb).mark_bar().encode(
x=alt.X("price")
.bin(maxbins=30)
.title("Price per night (dollars)"),
y=alt.Y("count()", title="Count"),
)
population_distribution
Fig. 10.3 Population distribution of price per night (dollars) for all Airbnb listings in Vancouver, Canada.#
In Fig. 10.3, we see that the population distribution has one peak. It is also skewed (i.e., is not symmetric): most of the listings are less than $250 per night, but a small number of listings cost much more, creating a long tail on the histogram’s right side. Along with visualizing the population, we can calculate the population mean, the average price per night for all the Airbnb listings.
airbnb["price"].mean()
154.5109773617762
The price per night of all Airbnb rentals in Vancouver, BC is $154.51, on average. This value is our population parameter since we are calculating it using the population data.
Now suppose we did not have access to the population data (which is usually the
case!), yet we wanted to estimate the mean price per night. We could answer
this question by taking a random sample of as many Airbnb listings as our time
and resources allow. Let’s say we could do this for 40 listings. What would
such a sample look like? Let’s take advantage of the fact that we do have
access to the population data and simulate taking one random sample of 40
listings in Python, again using sample.
one_sample = airbnb.sample(n=40)
We can create a histogram to visualize the distribution of observations in the sample (Fig. 10.4), and calculate the mean of our sample.
sample_distribution = alt.Chart(one_sample).mark_bar().encode(
x=alt.X("price")
.bin(maxbins=30)
.title("Price per night (dollars)"),
y=alt.Y("count()").title("Count"),
)
sample_distribution
Fig. 10.4 Distribution of price per night (dollars) for sample of 40 Airbnb listings.#
one_sample["price"].mean()
153.48225
The average value of the sample of size 40 is $153.48. This number is a point estimate for the mean of the full population. Recall that the population mean was $154.51. So our estimate was fairly close to the population parameter: the mean was about 0.7% off. Note that we usually cannot compute the estimate’s accuracy in practice since we do not have access to the population parameter; if we did, we wouldn’t need to estimate it!
Also, recall from the previous section that the point estimate can vary; if we
took another random sample from the population, our estimate’s value might
change. So then, did we just get lucky with our point estimate above? How much
does our estimate vary across different samples of size 40 in this example?
Again, since we have access to the population, we can take many samples and
plot the sampling distribution of sample means to get a sense for this variation.
In this case, we’ll use the 20,000 samples of size
40 that we already stored in the samples variable.
First we will calculate the sample mean for each replicate
and then plot the sampling
distribution of sample means for samples of size 40.
sample_estimates = (
samples
.groupby("replicate")
["price"]
.mean()
.reset_index()
.rename(columns={"price": "mean_price"})
)
sample_estimates
| replicate | mean_price | |
|---|---|---|
| 0 | 0 | 187.00000 |
| 1 | 1 | 148.56075 |
| 2 | 2 | 165.50500 |
| 3 | 3 | 140.93925 |
| 4 | 4 | 139.14650 |
| ... | ... | ... |
| 19995 | 19995 | 198.50000 |
| 19996 | 19996 | 192.66425 |
| 19997 | 19997 | 144.88600 |
| 19998 | 19998 | 146.08800 |
| 19999 | 19999 | 156.25000 |
20000 rows × 2 columns
sampling_distribution = alt.Chart(sample_estimates).mark_bar().encode(
x=alt.X("mean_price")
.bin(maxbins=30)
.title("Sample mean price per night (dollars)"),
y=alt.Y("count()").title("Count")
)
sampling_distribution
Fig. 10.5 Sampling distribution of the sample means for sample size of 40.#
In Fig. 10.5, the sampling distribution of the mean has one peak and is bell-shaped. Most of the estimates are between about $140 and $170; but there is a good fraction of cases outside this range (i.e., where the point estimate was not close to the population parameter). So it does indeed look like we were quite lucky when we estimated the population mean with only 0.7% error.
Let’s visualize the population distribution, distribution of the sample, and the sampling distribution on one plot to compare them in Fig. 10.6. Comparing these three distributions, the centers of the distributions are all around the same price (around $150). The original population distribution has a long right tail, and the sample distribution has a similar shape to that of the population distribution. However, the sampling distribution is not shaped like the population or sample distribution. Instead, it has a bell shape, and it has a lower spread than the population or sample distributions. The sample means vary less than the individual observations because there will be some high values and some small values in any random sample, which will keep the average from being too extreme.
Fig. 10.6 Comparison of population distribution, sample distribution, and sampling distribution.#
Given that there is quite a bit of variation in the sampling distribution of the sample mean—i.e., the point estimate that we obtain is not very reliable—is there any way to improve the estimate? One way to improve a point estimate is to take a larger sample. To illustrate what effect this has, we will take many samples of size 20, 50, 100, and 500, and plot the sampling distribution of the sample mean. We indicate the mean of the sampling distribution with a vertical line.